시작하기에 앞서, 아래 글을 참고하면 좋을 듯 하다.
[EDM] #19. 가장 빠른 음악 장르, 스피드 코어 / SpeedCore (late 90s~)
* 듣는 이에 따라서 불쾌감을 느끼실 수 있습니다 * * 만약 아니라면 변태임이 분명하다 * 새삼스럽게 한 가지 짚고 넘어가 보자면, EDM은 Electronic Dance Music이다. 중간의 Dance가 존재하는 이상, 적어
coldhearted-sirius-alpha-22.tistory.com
오늘의 목표는 다음과 같다 :

1) 19776 Hz가 음역대로 얼마인지?
2) 스피드 코어에 관한 실험 및 고찰
[ 배경 지식 및 표기 ]
시작하기 전에 앞서, 매우매우 간단한 음향악적 지식에 대해 알고 가자.
:: 옥타브 ::
우선, '옥타브(Octave)'가 무엇인지는 많이 들어봤을 것이라 생각한다.
문어(Octopus)에도 나오는 OCT는 숫자 8을 의미하며,
음악에서는 쉽게 말해 도 부터 다음 도까지의 거리를 의미한다.
이 사이에는 흔히 말하는 '도레미파솔라시', 즉 'CDEFGAB'가 존재한다.
흔히 사용하는 표기 방법이 있는데,
C4를 가온 도(=노래방 기준 2옥 도)로 하여 표기하는 방법이다.
남자들이 좋아하는(?) 고음곡들을 예시로 들어보자.
천년의 사랑 : 노래방 기준 3옥타브 레 = D5
바람기억 : 3옥타브 레# = D#5
She's gone : 3옥타브 솔 = G5
이는 낮은 음자리표(피아노 칠 때, 왼손이 위치한 디폴트값(?))의 기본 도를 1옥타브라고
기준을 두었기 때문이며, 정확히는 모르겠지만 성악과 연관있지 싶다...
:: 7음계와 12음계 ::
도레미파솔라시도는 각각 일정한 '정수비'의 진동수로 이루어져있다.
예컨대, 도 : 미 의 진동수 비는 4:5로 일정하며,
도 : 파의 진동수 비는 3:4로 일정하다.
이렇게 정수비로 딱딱 맞아 떨어지는 친구들을 한 스케일로 잡는 방식이 "7음계"이다.
그러나 실제로 피아노를 보면, 도레미파솔라시를 제외한 '검은 건반'들이 존재한다.
검은 건반인 도#, 레#, 파#, 솔#, 라#까지 포함하면 한 옥타브에는 총 12개의 음정이 존재하게 된다.
이들을 포함한 스케일을 "12음계"라 하며, 각 음계 간의 사이(음정, interval)를 '반음(semitone)'이라 칭한다.
세상에는 여러 스케일이 있지만, 보통은 12음계가 표준처럼 사용되니
12음계를 기준으로 설명하겠다.
[ Note to Frequency / Frequency to Note ]
우선 여러분들도 아시다싶이, 소리 역시 공기의 '진동'이다.
그리고, 초당 몇 회 진동하는가(=Hz, 초 당 진동수)는 음정의 높낮이(Pitch)에 영향을 미친다.
가장 간단한 원리를 설명하자면,
4옥타브 A와 5옥타브 A, 그러니까 한 옥타브(라 부터 다음 라)까지의 진동수는 정확하게 2배 차이난다.
즉, 흔히 악기 튜닝의 기준이 되는 A4는 440Hz이고,
그 다음 옥타브의 A5는 880Hz라는 뜻이다.
간단한 증명 과정은 아래와 같으니, 그냥 보고 넘기자 :
C3 : E3 : G3 = 4 : 5 : 6
G3 : B3 : D4 = 4 : 5 : 6
(옥타브는 임의로 설정했다. 누구 맘대로? 내 맘대로)
C3 : D4 = 4 : 9 이고, C4 : D4 = 8 : 9 이므로,
C3 : C4 = 4 : 8
이를 12음계로 확대해보면 다음과 같다.

여기서 f는 진동수, f_0는 기준 음계(A4), f_12를 한 옥타브 위의 음계 (A5)라 하면
위와 같은 식이 성립한다.
우리는 여기서 한 반음 단위의 결과가 궁금하므로, 아래와 같이 표현할 수 있다.

이게 얼마나 말이 되는지는? C4와 E4 (n=4)의 예시로 확인해보자.

놀랍게도 C4와 E4의 비율이 4:5라는 점을 알 수 있다!
놀랍다기 보다는, 위의 결과로 일반화된 식을 유도했다는게 맞다고 볼 수 있겠지만.
아무튼 이 단락에서 중요한 것은, 아래의 식이다.

그리고 우리는 기준점으로 A4 = 440 Hz를 사용할 것이다.
[ 계산 : 19776 Hz ]
19776 Hz는 목표 음계의 진동수, A4 = 440 Hz 이므로, 긴 말 없이 바로 시작해보자.

이 식을 계산해서 나오는 n을 알면, A4로부터 몇 반음만큼 위에 있는 음계인지 알 수 있다.
이걸 계산기로 계산하신다구요? 미쳤어요?
그냥 그래프 써요 우리...

좋아. 근사값으로 치자면, n은 65와 66 사이의 어딘가이다.
A4에서 65, 혹은 66 세미톤만큼 올라간 음은...
D9 혹은 D#9 그 사이일 것 같다.
7옥타브 레, 7옥타브 레# 그 사이 19776Hz 짧은 시간(당 진동수) 되시겠다.
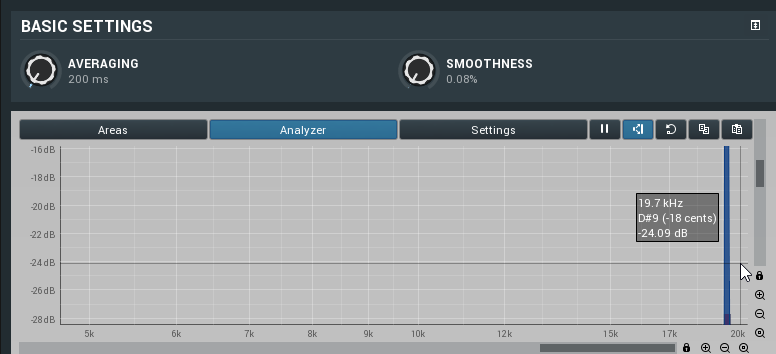
아 근데 다 구하고 나니까 그냥 이런 편한 방법이 있었다
이런 젠장.
어쨋거나 계산 결과와 분석 결과 D#9라는, 대충 납득할만한 결과가 나왔다.
한 김에 하나만 더 구해보자.
사람의 가청 주파수인 20,000 Hz는 음계로 얼마일까?
안타깝게도, 역시 D#9이다.
어쩔 수 없다, 자연계의 소리는 연속적이기 때문에
조금 높은 D#9와 조금 낮은 D#9와 온갖 D#9가 있을 뿐이다.
이렇게, 첫 번째 분석(?)이 끝났다.
이제 다음에는 하이퍼 톤에 관한 고찰이다.
>> 도움 받은 자료들 <<
https://doodle-ns.tistory.com/12
[주관적인 화성학] 2. 7음계와 12음계의 탄생과 평균율
주의: 이 시리즈는 독자적으로 화성학을 연구하며 알게 된 것들을 바탕으로, 실제 화성학 이론을 주관적으로 해석한 내용입니다. 정식 화성학 이론과는 다를 수 있습니다. 7음계의 탄생 7음계란
doodle-ns.tistory.com
https://pages.mtu.edu/~suits/notefreqs.html
Frequencies of Musical Notes, A4 = 440 Hz
Tuning Frequencies for equal-tempered scale, A4 = 440 Hz Other tuning choices, A4 = Speed of Sound = 345 m/s = 1130 ft/s = 770 miles/hr More about Speed of Sound ("Middle C" is C4 ) NoteFrequency (Hz)Wavelength (cm) C0 16.35 2109.89 C#0/Db0 17.32 1991.
pages.mtu.edu
'수상한 뻘짓의 세계 > 뻘짓의 세계' 카테고리의 다른 글
| [냉혹한 뻘짓의 세계] #03. 왜 완전 음정은 1도 4도 5도 8도밖에 없을까? (0) | 2022.01.25 |
|---|---|
| [냉혹한 뻘짓의 세계] #02. 음정과 헤르츠의 관계, 그리고 하이퍼톤 (2) (0) | 2022.01.12 |
| [냉혹한 뻘짓의 세계] #00. 목록 (0) | 2022.01.11 |

