[번역] [britannica] 소리(sound)의 구성 요소들
원글) https://www.britannica.com/science/sound-physics
^) 이해의 편의 및 참고 사항
+) 번역한 '본인'의 코멘트, 즉 역자 주
- 본 글에서의 '필자'는 원글 작성자를 의미함
- 원활한 전달을 위해, 일부 불필요한 내용 제거 및 의역 포함되었음 (번역체 -> 자연스러움 목적)
Sound
Sound(소리)는 탄성 물질을 매개체로 하여 전파되는 평형 상태의 기계적인 교란을 의미한다. 사람의 관점에서는 '귀를 통해 받아들이는' 감각으로 정의할 수도 있지만, 이는 불완전하고 제한적인 정의이다. 왜냐하면, 일부 동물이나 장비에 의해 만들어진 소리 중 사람의 귀에 들리지는 않는 소리들 역시 존재하기 때문이다.
음향을 이해하기 위해서는 소리의 파형(wave)의 속성을 알아볼 필요가 있다. 파형에는 두 종류의 기본형이 있는데, 만들어지는 방법에 따라 Transverse(횡파)와 Longitudinal(종파)로 구분한다. 횡파(누군가가 줄의 끝을 붙잡고 위아래로 흔드는 모습을 생각해보자)는 파의 전파 방향과 입자의 진동 방향이 수직이 된다. 빛이나 라디오 전파처럼 어딘가로 전파되는 파형이 흔히 이 모습을 띈다.
그에 반해, 파의 전파 방향과 입자의 진동 방향이 일치하는 파형을 종파라고 한다. 종파는 스프링을 앞뒤로 밀고 당길 때 보이는 모습과 비슷하며, 공기를 구성하는 입자들이 파동의 진행 방향을 따라 '밀고 밀리는(이를 압축된다고 표현하여 Compressional wave라고도 한다)' 현상과 같다.

따라서, 종파는 매질이 비교적 뭉쳐있는 '밀'과 매질의 밀도가 옅은 '소'로 나누어지며, 일정한 속도로 전파되게 된다.
Plane Waves
공간을 주파하는 소리를 관찰하기 위해서는, 평면상을 주파하는 개별 파형에 대한 접근이 필요하다. 물론 이 파형이 전체 소리를 대표한다고 할 수는 없지만 말이다. 어떤 소리의 한 단일 주파수 파동은 어떤 물체를 두드렸을 때 발생하는 순수한 파형처럼 들릴 것이다. 이를 이론적인 모델로 삼으면 소리의 많은 부분을 이해하는데 도움이 될 것이다.
Wavelength, Period, and Frequency

Figure1C는 Figure 1B의 또다른 표현이다. 소리를 사인함수와 같은 주기 함수로 표현하자면, 소리의 파형에서 압력(=밀도)의 변화는 일정 간격마다 반복됨을 알 수 있다. 이 간격을 'Wavelength (파장)'라고 하며, λ로 표기한다. (단위는 미터(metres, m))
한 번의 파동은 공기를 통해 전파되면서 어떤 지점을 일정한 시간동안 통과하게 되는데, 이를 'Period(주기)'라고 하며 T로 표기한다 (단위는 초(seconds, s)). 그렇게 파동이 1초동안 반복되는 횟수를 'Frequency(주파수/진동수, f)'라고 하며, 초당 반복되는 횟수를 'Hertz(헤르츠)' 단위로 정의하였다.
파동의 주파수와 주기는 서로 반비례 관계에 있으므로, 아래 (1)의 식이 성립한다.
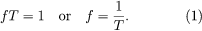
따라서, 높은 주파수의 소리는 짧은 주기를 갖게 되며, 낮은 주파수는 긴 주기를 갖게 된다. 예를 들어, 20Hz의 파동은 0.05초의 주기를 갖게 될 것이며(20 wavelength / sec * 0.05 sec/wavelength = 1), 20kHz의 파동은 0.00005초의 주기를 갖게 될 것이다. 사람은 20~20,000 헤르츠 사이의 주파수를 감지할 수 있다. 파동의 물리적인 성질은 'pitch (음정)'으로 나타나므로, 높은 주파수의 소리는 더 높은 음정으로 받아들여진다. 또한 파장, 주기, 주파수, 파동의 전파 속도(S)는 다음과 같은 관계를 갖는다.
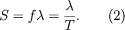
Amplitude and intensity
[수학적인 계산]
Figure 1A처럼 일정한 압력을 유지하는 경우는, 아무런 소리가 없는 공기의 상태와 같다. 음파를 구성하는 압력의 변화 등이 발생할 때, 공기중에는 압력의 차이에 의한 출렁임(진동)이 발생한다. 이때 진동의 강도는 파동의 'Amplitude(진폭)'와 같다. 진폭은 A로 표기하며, pascal(pa) 혹은 N/m^2 으로 정의한다.
평면상에 놓여진 한 파동은 수학적으로 '파동 함수(Wave equation)'로 나타낼 수 있다.
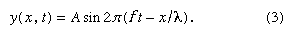
이 함수는 주기가 λ이고 어떤 Velocity(소리의 속도, S)를 갖는 소리를 주기함수로 나타낸 것이다 (x는 x축으로 평행이동). 소리의 진폭은 Intensity(소리의 강렬함, 이 글에서는 '강도'로 통일)와 관련되며, 이를 귀에서는 소리의 'loudness(세기)'로 인식한다. 강도는 파동의 전파 방향에 수직인 단위 면적에 가해지는 평균 에너지로 정의된다. 이를 식으로 나타내면 아래와 같다.
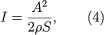
여기서 I는 강도, ρ는 평형 상태일 때 매질(공기)의 밀도이며, S는 소리의 전파 속도이다. I는 watt(와트)/m^2으로 나타내지며, 이는 전자/기계공학에서의 표준 단위이다.
표준 상태의 대기는 10^5 파스칼의 대기압을 갖는다*. 사람의 귀가 인식할 수 있는 가장 낮은 압력의 변화는 0.00005 파스칼이며, 고통을 느끼기 시작하는 변화량은 10 파스칼이다. 일반적인 소리는 대기압에 비하면 매우 낮은 압력의 변화를 나타낸다. 일반적으로 공기중에서 소리는 에너지 손실과 형태의 변화가 최소화되는 직선적으로 전파된다. 하지만, 진폭이 100 파스칼을 넘어가면(이는 대기압의 1,000분의 1에 해당한다) 소리의 파형에 비선형적인 변화가 상당히 발생한다.
(* 대기압 = 101325 pascal = 101.325 kPa)
이러한 변화는 공기 입자가 정현파*에 의해 발생한 압력에 영향을 받기 때문이다. 만약 파동의 진폭이 작다면, 공기 입자에 전달되는 압력의 변화 또한 작거나 거의 없을 것이다. 하지만 반대의 경우에서는, 공기 입자의 밀도가 충분히 낮아지기도 전에 이를 초과하는 압력이 가해지게 된다. 이상기체 방정식(PV=nRT)에서도 이를 알 수 있는데, 기체의 부피가 1.5배로 증가할 때 압력은 3분의 1만 감소하지만, 부피가 절반으로 감소하게 되면 압력은 2배나 증가하게 된다. 그 결과 과잉 압력이 발생하게 되는데, 이는 어디까지나 진폭이 100 파스칼을 넘는 경우에만 중요하다.
(* 정현파 : sin, cos 함수와 같은 주기 함수. 여기서는 소리의 파동이라고 보시면 될듯)
The Decibel Scale
귀가 소리를 받아들이는 메커니즘은 비선형적이기에, 작은 압력차와 큰 압력차를 가진 파동 모두에 반응할 수 있다. 따라서, 귀는 강도의 변화가 작은 경우에 더 효율적으로 받아들인다. 귀가 비선형적인 파동에도 반응하기에, 비선형적인 스케일은 소리의 강도로 표현되는것이 편하다. 이를 위해서 sound intensity level, 혹은 아래와 같이 정의된 decibel level(데시벨 레벨)을 사용한다.
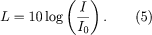
여기서 L은 데시벨(I는 W/m^2으로 정의된 Intensity)을 의미한다.여기서 분모의 I0는 0데시벨에 해당하며, 1,000 헤르츠의 주파수를 가지며 인식될 수 있는 제일 낮은 크기의 소리이다. 귀가 선형적인 파동(즉 I값이 낮을 때)에 더 잘 반응하기에, 위의 식은 선형적인 수식보다 더 실용적이라고 할 수 있다.
데시벨은 로그 스케일로 정의되며, 주요한 특징 중 하나는 절대 강도(absolute intensity, 식 (5)의 I값) n배로 늘어날 때 실제 소리의 크기(데시벨)은 I의 n승배로 증가한다는 점이다. 즉, 절대 강도가 10^-12에서 10^-11 (W/m^2)로 증가하였거나 10^-1에서 1 (W/m^2)으로 증가하였다면, 데시벨은 10 dB 증가함을 의미한다. 소리의 강도와 데시벨과 관련된 표는 아래에 정리하였다.
0데시벨은 귀가 인지할 수 있는 가장 낮은 소리이고, 120~130데시벨은 귀가 고통을 느끼기 시작하는 범위이다.
| 데시벨 (dB) | 소리의 강도 (Intensity) (10^n에서 n) | 예시 |
| 130 | 1 | 근거리에서 대포를 발사했을 때 |
| 120 | 0 | 앰프를 통한 락 음악, 제트 엔진 옆 |
| 110 | -1 | 관중석에서 들리는 커다란 오케스트라 음악 |
| 100 | -2 | Saw 파형 |
| 90 | -3 | 버스, 트럭 내부에서 느껴지는 소음 |
| 80 | -4 | 자동차 내부에서 느껴지는 소음 |
| 70 | -5 | 일반적인 거리의 소음, 커다란 휴대폰 벨소리 |
| 60 | -6 | 일반적인 대화, 사무실 소리 등 |
| 50 | -7 | 레스토랑, 개인 사무실 |
| 40 | -8 | 조용한 방 |
| 30 | -9 | 전시관, 침실 |
| 20 | -10 | 라디오/TV/음악 스튜디오 |
| 10 | -11 | 방음실 |
| 0 | -12 | 거의 인지할 수 없는 소리 |
데시벨은 비선형적인 스케일이므로 값을 직접적으로 계산할 수 있다. 오디오 시스템이나 건축 공학등의 다른 산업에서는 소리의 단위로 dB를 자주 사용한다.
:: 참고 할 만한 자료들 ::
https://www.britannica.com/science/sound-physics/The-decibel-scale
근데 이런 것 까지 알 필요가 있을까?